萝莉 在线

“铺砌”是数学规模的一个已取得充分探索的成见。永远以来，数学家们一直在盘考什么样的几何格局不错通过组合而无漏洞地铺满名义。惩处这类问题的典型念念路，是使器用有拐角的平面格局。关联词，这么的格局在当然界中并不常见。

当今，在一项于近期发表在PNAS Nexus上的盘选取，来自布达佩斯本事与科技大学和牛津大学的数学家发现了一类新的格局，不错在莫得任何拐角的情况下铺砌空间。他们将这类由圆角组成的新几何格局称为“软细胞”（soft cell）。更神奇的是，这些柔嫩的格局在当然界随地可见。

将拐角酿成圆角

铺砌可分为周期性和非周期性铺砌。举例，三角形、正方形、六边形，不错周期性地铺砌二维空间，再比如立方体不错周期性地铺砌三维空间。

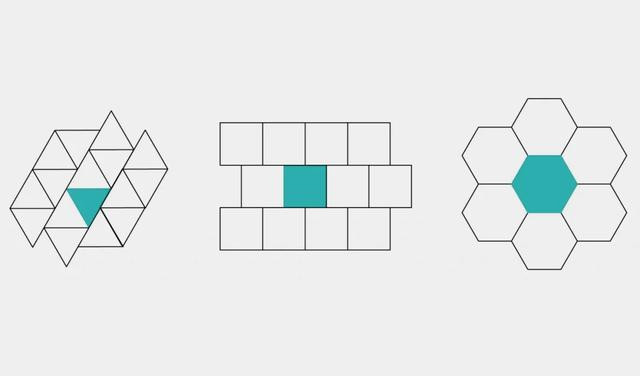
三角形、正方形、六边形不错周期性地铺砌平面。（图/道理）

比较之下，寻找非周期性铺砌的例子要艰苦多，因为它条款由这些格局组成的举座图案，无法通过平移或旋转来收复。彭罗斯铺砌即是一个有名的非周期性铺砌示例。

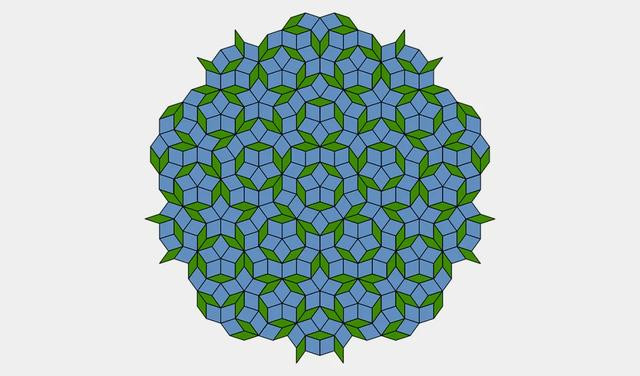
由两种菱形组成的彭罗斯铺砌。（图/Wikipedia）

在新的盘选取，Gábor Domokos偏握共事接头了的是“概况”的周期性铺砌。但特殊的是，他们探讨了有着“圆角”的几何格局的铺砌问题。

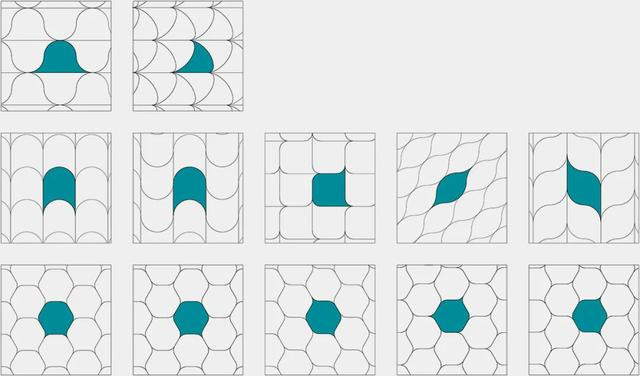
新盘考将一类新的不错无漏洞铺砌空间的格局定名为软细胞。第一排露出了等效于成例三角形的软铺砌，第二行露出了等效于长方形的软铺砌，第三行露出了等效于六边形的软铺砌。（图/Domokos et. al. / PNAS Nexus）

在二维空间中，当让一些传统的铺砌系统（比如三角形、长方形、六边形、立方体）的边转折，拐角变“圆”时，这些被“软化”过的格局就无法再以不留漏洞的时势铺砌空间了。但是，当让一些拐角变“尖”时，就又不错作念到无漏洞铺砌了。

在这个进程中，盘考东说念主员尽可能地最小化“尖角”的数目。通过这么作念，他们创造出了一类具有不同铺砌特质的新数学格局，并将这些领有最极少量的拐角、能无漏洞铺砌空间的几何格局定名为“软细胞”。

软细胞领有最极少量的尖角，而且能莫得漏洞地铺砌空间。在当然界和树立中王人存在有着两个尖角的软细胞的例子。第1列露出的是几何软细胞示例，第2、3列露出的是当然界的软细胞示例，第4列露出的是树立师扎哈·哈迪德的树立策划。（图/Wikimedia Commons， Google Earth， Krisztina Regős.）

他们发现，在二维空间里，所有的软细胞王人必须至少有两个“尖角”。在肌细胞、斑马条纹、河流岛屿的格局、洋葱鳞茎的层，甚而在树立策划中，王人能找到这么的铺砌模式。

在三维空间中，软细胞变得愈加复杂和道理——它们不错全王人莫得尖角，却能无漏洞地铺砌所有这个词空间，鹦鹉螺的壳腔即是一个很好的例子：从鹦鹉螺的横截面来看，其壳室看起来像是有着两个尖角的二维软细胞，但其本色的三维腔室根底莫得任何拐角。

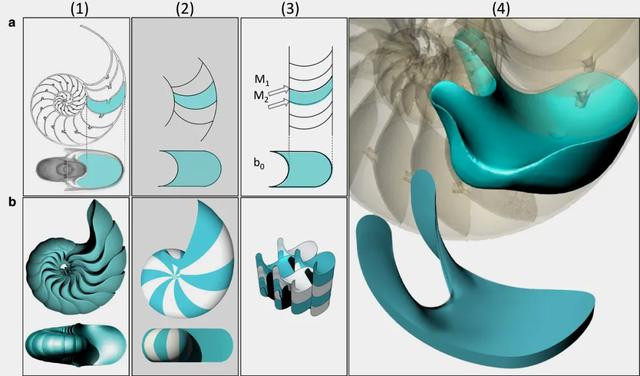
鹦鹉螺腔室的几何格局。（图/Domokos et. al. / PNAS Nexus）

开启新的问题

其实，当一些树立师想要幸免拐角时，他们会凭直观创造出这些格局，比如有名的树立师包括扎哈·哈迪德就频繁这么作念。

新的发现开启了几何学和生物学的一系列问题。目下，盘考东说念主员尚不明晰大当然是若何期骗这些“柔嫩”的格局来完结几何复杂性的。但他们推断，当然界之是以平方会幸免拐角，可能是因为这些扭折在形变能上的老本很高，并有可能是结构性过失的着手。

封面图&首图：Content Pixie / Unsplash萝莉 在线